Quadrilaterals and its Types

What is rhombus.

Diagonals of a square bisect each other at _____

A quadrilateral has how many diagonals.

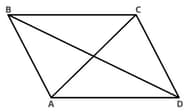
Find the opposite vertices of quadrilateral given below

$P\left(-2,2\right), Q\left(8,2\right), R\left(4,-4\right),S\left(-6,-4\right)$ are the vertices of a quadrilateral. Find the opposite vertices of quadrilateral

$A\left(-2,2\right), B\left(8,2\right), C\left(4,-4\right),D\left(-6,-4\right)$ are the vertices of a quadrilateral. Find the opposite vertices of quadrilateral

A quadrilateral with exactly two sides parallel is a _____.

The diagonals of a square have mutually bisecting diagonals.

The diagonals of a kite have mutually bisecting diagonals.

All the sides of rhombus are equal.

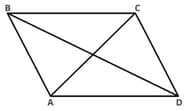
Identify all pairs of the opposite vertices. How many pairs of opposite vertices?

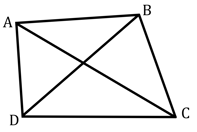
Define opposite vertices of a quadrilateral.

Look at the rhombus shaped photo frame. The measure of the shorter diagonal is $ {\frac{3}{4}}^{\text{th}}$the longer diagonal which is 40 cm long. The length of lace required to decorate along its boundary is _____ cm.

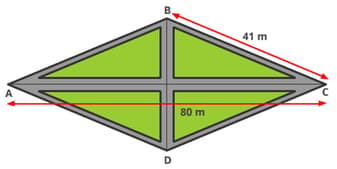
A park is shaped like a rhombus with pathways to walk as shown. The shortest distance from the centre of the park to point D is _____m.

In the rhombus ABCD with side length $ 20$ cm, the diagonals are in the ratio $ 3:4.$ The length of the longer diagonal is _____ cm.

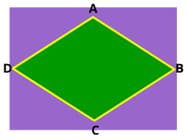
In rhombus ABCD, we have measure of ∠B is 3 times that of ∠A.

The measure of ∠D is _____$ °$.

ABCD is a rhombus where side $ \text{AB}=4x-11$ and side $ \text{AD}=3x+6$. The measure of side $ \text{BC}=$_____ units.

ABCD is a rhombus. The measure of $ \angle \text{BCA}=3x-2$ and the measure of $ \angle \text{ACD}=14+x$. The measure of $ \angle \text{BCD}=$_____$ °$.

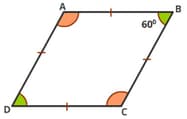
Quadrilateral ABCD is a rhombus. If the measure of $ \angle B=60°$ then the measure of $ \angle C=$_____$ °$.

(Write the answer in number format only.)